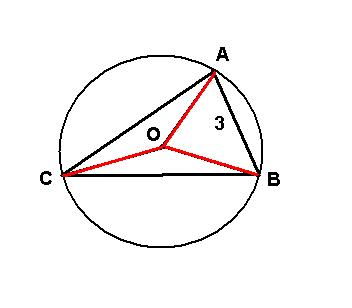
Notam cu R=raza si cu O centrul cercului si avem:
In ΔOCA, <OCA=<OAC pentru ca OC=OA=OB=R ⇒<COA=180-2*<OCA
in ΔOCB, <OCB=<OBC ot ca OC=OB=OA=R ⇒ <COB=180-2*<OCB
⇒<AOB=360-<COA-<COB=360-180+2*<OCA-180+2*<OCB
<AOB=2*<OCA+2*<OCB=2*(<OCA+<OCB)=2*30
<ACB=30=<OCA+<OCB
⇒<AOB=60°
si avem formula:
AB=2*R*sin [tex] \frac{<AOB}{2} [/tex]
3=2*R* sin (60/2)
3=2*R*sin 30°
3=2*R*1/2
3=R